Simplest Chaotic System with a Hyperbolic Sine
Oscillating circuit using a TL084 op amp.
It's similar to Chua's Circuit with chaos, bifurcation, etc.
The two LEDs are there for use without an oscilloscope...here is a version by Sprott without LEDs: http://sprott.physics.wisc.edu/pubs/paper352.htm
I hate breadboards, oscillating circuits never seem to work, so here is my point-to-point wired beauty:
Ground clips from oscilloscope probes went to gathered ground wires from the op amp (which actually came off the positive output pins!). Clipped the probes onto the legs of a couple of the ceramic capacitors to take a reading.
Connected the two 9 volt batteries together and then ran positive wire and negative wire from the appropriate free battery posts.
Simple layout:
Good old TL084 pinout. I think I actually used TL084ACN (newer version):
Resistor R1 = 13kΩ,
All other resistors are 10kΩ.
All the capacitors are 0.01µF monolithic ceramic capacitors.
At first I kept getting the 'flying hotdog' which in the report of Liu, Sprott, Wang and Ma they accepted as a valid output. I was only getting it when nothing else was responding. Here is a pic of it, but it's not cool or interesting:

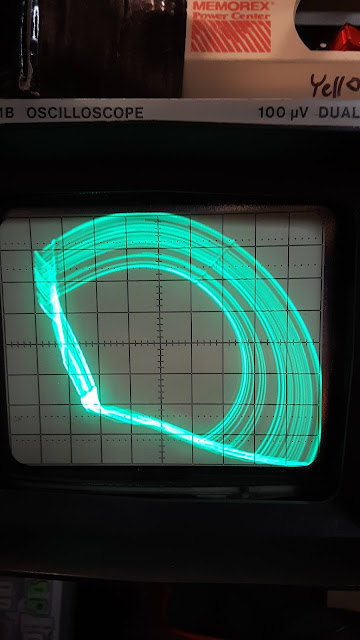
This is where the awesomeness starts! I had to touch my finger to the negative 9v battery output to get this circuit ring (actually it's a jerk circuit, so maybe it jerks?). This is because I didn't put a potentiometer at the double 9volt battery supply. It was full +/- 9 volts.

It is close to a chaotic attractor associated with a type I class 3 eigenvalue patttern.
This mimics (well, gets close anyway to) another valid response according to Liu et al's paper. It rarely showed up, because I wasn't varying the power supply much:
Chaos is a steady-state behavior possible in any nonlinear continuous
system, if its order is above 2 in a forced circuit; or 3 in certain autonomous
circuits.
We're just waiting for the thunder storm to pass by.