Chua Circuit Bibliography

Chua Circuit Bibliography 

(working links as of 12/18/2019)

I'm continuing with oscillating circuit experiments. More inductors are being delivered in the next few weeks. This is a list of Chua Diode and Circuit articles with working (free) links. Some are pretty advanced and focus on equations and synchronization--the earlier the year of publication the more physical circuit-based (fun) it will be if you're building your own circuits and playing with oscilloscopes or LTspice:

·          Aguirre, L.A. [1995] "The use of identified models in the control of a chaotic circuit," 1995 IEEE International Symposium on Circuits and Systems (Cat. No.95CH35771). IEEE. Part vol.2, pp.1528-1531.

·          Aguirre, L.A., Souza, A.V.P. [1998] "An algorithm for estimating fixed points of dynamical systems from time series," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.8, no.11, pp.2203-2213.

·          Aguirre, L.A., Torres, L.A.B. [1997] "Fixed point stability analysis of Chua's circuit: a case study with a real circuit," Journal of Circuits Systems & Computers, vol.7, no.2, pp.111-115.

·          Aissi, C., Fadul, F. [1997] "Chaos in conditionally reset linear systems," Journal of Circuits Systems & Computers, vol.7, no.3, pp.177-189.

·          Alexeyev, A.A., Osipov, G.V., Shalfeev, V.D. [1995] "Effects of square-wave modulation on CNN patterns," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.42, no.10, pp.700-705.

·          Algaba, A., Freire, E., Gamero, E., Rodriguez-Luis, A.J. [1999] "On the Takens-Bogdanov bifurcation in the Chua's equation," IEICE Transactions on Fundamentals of Electronics Communications & Computer Sciences, vol.E82-A, no.9, pp.1722-1728.

·          Altman, E.J. [1993] "Normal Form Analysis of Chua`s Circuit with Applications for Trajectory Recognition," IEEE Transactions on Circuits & Systems II-Analog & Digital Signal Processing, vol.40, no.10, pp.675-682.

·          Alvarez, J., Alvarez, J., Velasco, M. [1997] "Approximate model-matching for nonlinear systems with a small time-delay; application to a chaotic Chua circuit," Proceedings of the 36th IEEE Conference on Decision and Control (Cat. No.97CH36124). IEEE. Part vol.2, pp.1631-1636.

·          Anishchenko, V.S., Kapitaniak, T., Safonova, M.A., Sosnovzeva, O.V. [1994] "Birth of double-double scroll attractor in coupled Chua circuits," Physics Letters A, vol.192, no.2-4, pp.207-214.

·          Anshan, H. [1988] "A Study of the Chaotic Phenomena in Chua's Circuit," Proceedings of 1988 IEEE International Symposium on Circuits and Systems (Cat. No.88CH2458-8). IEEE. vol.1, pp.273-276.

·          Arena, P., Baglio, S., Fortuna, L., Manganaro, G. [1995] "Chua's circuit can be generated by CNN cells," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.42, no.2, pp.123-125.

·          Arena, P., Baglio, S., Fortuna, L., Manganaro, G. [1995] "Simplified scheme for realisation of Chua oscillator by using SC-CNN cells," Electronics Letters, vol.31, no.21, pp.1794-1795.

·          Arena, P., Baglio, S., Fortuna, L., Xibilia, M.G. [1995] "Chaotic time series prediction via quaternionic multilayer perceptrons," 1995 IEEE International Conference on Systems, Man and Cybernetics. Intelligent Systems for the 21st Century (Cat. No.95CH3576-7). IEEE. Part vol.2, pp.1790-1794.

·          Arena, P., Caponetto, R., Fortuna, L., Muscato, G., Xibilia, M.G. [1996] "Quaternionic multilayer perceptrons for chaotic time series prediction," IEICE Transactions on Fundamentals of Electronics Communications & Computer Sciences, vol.E79-A, no.10, pp.1682-1688.

·          Arena, P., Fortuna, L., Porto, D., Rizzo, A. [1999] "Self-organisation in arrays of nonlinear systems induced by chaotic perturbation: An experimental approach," ISCAS'99. Proceedings of the 1999 IEEE International Symposium on Circuits and Systems VLSI (Cat. No.99CH36349). IEEE. Part vol.5, pp.479-482.

·          Astakhov, V., Shabunin, A., Anishchenko, V. [1998] "Synchronization of self-oscillations by parametric excitation," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.8, no.7, pp.1605-1612.

·          Bartissol, P., Chua, L.O. [1988] "The Double Hook (Nonlinear Chaotic Circuits)," IEEE Transactions on Circuits & Systems, vol.35, no.12, pp.1512-1522.

·          Bernardo, M.Di [1996] "A purely adaptive controller to synchronize and control chaotic systems," Physics Letters A, vol.214, no.3-4, 13 May 1996, pp.139-144.

·          Berns, D.W., Moiola, J.L., Guanrong, C. [1998] "Predicting period-doubling bifurcations and multiple oscillations in nonlinear time-delayed feedback systems," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.45, no.7, pp.759-763.

·          Berns, D.W., Moiola, J.L., Guanrong, C. [1998] "Predicting period-doubling bifurcations in nonlinear time-delayed feedback systems," Proceedings of the 1998 IEEE International Symposium on Circuits and Systems (Cat. No.98CH36187). IEEE. Part vol.3, pp.619-622.

·          Biey, M., Bonani, F., Gilli, M., Maio, I. [1996] "Influence of the parasitics on the time delayed Chua's circuit," 8th Mediterranean Electrotechnical Conference. Industrial Applications in Power Systems, Computer Science and Telecommunications. Proceedings (Cat. No.96CH35884). IEEE. Part vol.1, pp.443-446.

·          Biey, M., Bonani, F., Gilli, M., Maio, I. [1997] "Qualitative Analysis of the Dynamics of the Time-delayed Chua's Circuit," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.44, no.6, pp.486-500.

·          Biey, M., Gilli, M., Maio, I., Premoli, A. [1998] "A computer program for accurate time-domain analysis of 1D-arrays of Chua's oscillators," Proceedings of the 1998 IEEE International Symposium on Circuits and Systems (Cat. No.98CH36187). IEEE. Part vol.3, pp.383-386.

·          Bonani, F., Gilli, M. [1999] "A harmonic balance approach to bifurcation analysis of limit cycles," ISCAS'99. Proceedings of the 1999 IEEE International Symposium on Circuits and Systems VLSI (Cat. No.99CH36349). IEEE. Part vol.6, pp.298-301.

·          Bonani, F., Gilli, M. [1999] "Analysis of stability and bifurcations of limit cycles in Chua's circuit through the harmonic-balance approach," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.46, no.8, pp.881-890.

·          Bonet, J., Pala, P., Milo, J.M. [1998] "A discrete-time approach to the steady state analysis of distributed nonlinear autonomous circuits," Proceedings of the 1998 IEEE International Symposium on Circuits and Systems (Cat. No.98CH36187). IEEE. Part vol.3, pp.460-464.

·          Bonet-Dalmau, J., Pala-Schonwalder, P., del Aguila-Lopez, F. [1999] "Steady state analysis of Chua's circuit with RLCG transmission line," ICECS'99. Proceedings of ICECS '99. 6th IEEE International Conference on Electronics, Circuits and Systems (Cat. No.99EX357). IEEE. Part vol.2, pp.819-822.

·          Broucke, M.E. [1987] "One Parameter Bifurcation Diagram for Chua's Circuit," IEEE Transactions on Circuits & Systems, vol.CAS-34, no.2, pp.208-209.

·          Brown, R. [1993] "Generalizations of the Chua Equations," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.40, no.11, pp.878-884.

·          Brucoli, M., Cafagna, D., Carnimeo, L., Grassi, G. [1996] "Hyperchaotic circuits for secure communications: an efficient synchronization technique," Proceedings of the Third IEEE International Conference on Electronics, Circuits, and Systems. ICECS '96 (Cat. No.96TH8229). IEEE. Part vol.2, pp.639-642.

·          Brucoli, M., Cafagna, D., Carnimeo, L., Grassi, G. [1998] "Synchronization of hyperchaotic circuits via continuous feedback control with application to secure communications," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.8, no.10, pp.2031-2040.

·          Brucoli, M., Cafagna, D., Carnimeo, L., Grassi, G. [1999] "Design of a hyperchaotic cryptosystem: based on identical and generalized synchronization," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.9, no.10, pp.2027-2037.

·          Brucoli, M., Carnimeo, L., Grassi, G. [1996] "On the dynamics of hyperchaotic circuits: a new synchronization approach," 8th Mediterranean Electrotechnical Conference. Industrial Applications in Power Systems, Computer Science and Telecommunications. Proceedings (Cat. No.96CH35884). IEEE. Part vol.1, pp.435-438.

·          Bykov, V.V. [1998] "On bifurcations leading to chaos in Chua's circuit," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.8, no.4, pp.685-699.

·          Calvo, O., Cartwright, J.H.E. [1998] "Fuzzy control of chaos," World Scientific. International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.8, no.8, pp.1743-1747.

·          Caponetto, R., Fortuna, L., Lavorgoa, M., Manganaro, G., Occhipinti, L.[1996] "Experimental study on chaotic synchronisation with non-ideal transmission channel," IEEE GLOBECOM 1996. Communications: The Key to Global Prosperity. Conference Record (Cat. No.96CH35942). IEEE. Part vol.3, pp.2083-2087.

·          Caponetto, R., Fortuna, L., Occhipinti, L., Xibilia, M.G. [1998] "Hyperchaotic dynamic generation via SC-CNNs for secure transmission applications," 1998 IEEE International Joint Conference on Neural Networks Proceedings. IEEE World Congress on Computational Intelligence (Cat. No.98CH36227). IEEE. Part vol.1, pp.492-496.

·          Chen, G. [1997] "On Some Controllability Conditions for Chaotic Dynamics Control," Chaos Solitons & Fractals, vol.8, no.9, pp.1461-1470.

·          Chen, G., Dong, X. [1993] "Ordering Chaos of Chua's Circuit-A Feedback Control Approach," Proceedings of 1993 IEEE International Symposium on Circuits and Systems, vol.4, pp.2604-2607.

·          Choi, I. [1994] "Interactive exploration of a chaotic oscillator for generating musical signals in real-time concert performance," Journal of the Franklin Institute, vol.331B, no.6, pp.785-818.

·          Chua, L.O. [1992] "A Zoo of Strange Attractors from the Canonical Chua's Circuits," Proceedings of the 35th Midwest Symposium on Circuits and Systems (Cat. No.92CH3099-9). IEEE. vol.2, pp.916-926.

·          Chua, L.O. [1993] "Global Unfolding of Chua's Circuit," IEICE Transactions on Fundamentals of Electronics Communications & Computer Sciences, vol.E76-A, no.5, pp.704-734.

·          Chua, L.O. [1994] "Chua's circuit: ten years later," IEICE Transactions on Fundamentals of Electronics Communications & Computer Sciences, vol.E77-A, no.11, Nov. 1994, pp.1811-1822.

·          Chua, L.O. [1995] "A glimpse of nonlinear phenomena from Chua's oscillator," Philosophical Transactions of the Royal Society of London a Mathematical & Physical Sciences, vol.353, no.1701, pp.3-12.

·          Chua, L.O., Huynh, L.T. [1992] "Bifurcation Analysis of Chua's Circuit," Proceedings of the 35th Midwest Symposium on Circuits and Systems (Cat. No.92CH3099-9). IEEE. vol.1, pp.746-751.

·          Chua, L.O., Lin, G-N. [1990] "Canonical Realization of Chua's Circuit Family," IEEE Transactions on Circuits & Systems, vol.37, no.7, pp.885-902.

·          Chua, L.O., Lin, G-n. [1991] "Intermittency in a Piecewise-linear Circuit," IEEE Transactions on Circuits & Systems, vol.38, no.5, pp.510-20.

·          Chua, L.O., Pivka, L., Wu, C-W. [1995] "A universal circuit for studying chaotic phenomena," Philosophical Transactions of the Royal Society of London a Mathematical & Physical Sciences, vol.353, no.1701, pp.65-84.

·          Chua, L.O., Wu, C.W., Huang, A., Zhong, G-Q. [1993] "A Universal Circuit for Studying and Generating Chaos. I. Routes to Chaos," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.40, no.10, pp.732-744.

·          Chua, L.O., Wu, C.W., Huang, A., Zhong, G-Q. [1993] "A Universal Circuit for Studying and Generating Chaos. II. Strange Attractors," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.40, no.10, pp.745-761.

·          Chua, L.O., Yang, T., Zhong, G-Q., Wu, C-W. [1996] "Synchronization of Chua's circuits with time-varying channels and parameters," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.43, no.10, pp.862-868.

·          Chua, LO., Komuro, M., Matsumoto, T. [1986] "The Double Scroll Family," IEEE Transactions on Circuits & Systems, vol.CAS-33, no.11, pp.1073-1118.

·          Civalleri, P.P., Gilli, M. [1999] "Analysis of nonlinear dynamic arrays, through spatial mode decomposition," ISCAS'99. Proceedings of the 1999 IEEE International Symposium on Circuits and Systems VLSI (Cat. No.99CH36349). IEEE. Part vol.5, pp.310-313.

·          Claussen, J.C., Mausbach, T., Piel, A., Schuster, H.G. [1998] "Memory difference control of unknown unstable fixed points: Drifting parameter conditions and delayed measurement," Physical Review E. Statistical Physics, Plasmas, Fluids, & Related Interdisciplinary Topics, vol.58, no.6, pp.7256-7260.

·          Corron, N.J., Hahs, D.W. [1997] "A New Approach to Communications Using Chaotic Signals," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.44, no.5, pp.373-382.

·          Cruz, J.M., Chua, L.O. [1992] "A CMOS IC Nonlinear Resistor for Chua's Circuit," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.39, no.12, pp.985-995.

·          Cruz, J.M., Chua, L.O. [1993] "An IC Chip of Chua`s Circuit," IEEE Transactions on Circuits & Systems II-Analog & Digital Signal Processing, vol.40, no.10, pp.614-625.

·          Dabrowski, A.M., Dabrowski, W.R., Ogorzalek, M.J. [1993] "Dynamic Phenomena in Chain Interconnections of Chua's Circuits," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.40, no.11, pp.868-871.

·          Daqin, Z., Zhong, R., Shi, L., Shenchu, X. [1996] "Anti-jamming of chaotic signals," ICSP '96. 1996 3rd International Conference on Signal Processing Proceedings (Cat. No.96TH8116). IEEE. Part vol.1, pp.261-263.

·          Dedieu, H., Kennedy, M.P., Hasler, M. [1993] "Chaos Shift Keying: Modulation and Demodulation of a Chaotic Carrier Using Self-synchronizing Chua`s Circuits," IEEE Transactions on Circuits & Systems II-Analog & Digital Signal Processing, vol.40, no.10, pp.634-642.

·          Dedieu, H., Ogorzalek, M.J. [1997] "Identifiability and identification of chaotic systems based on adaptive synchronization," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.44, no.10, pp.948-962.

·          Delgado-Restituto, M., Linan, M., Rodriguez-Vazquez, A. [1996] "IC design for spread spectrum communication exploiting chaos," 1996 IEEE International Symposium on Circuits and Systems. Circuits and Systems Connecting the World, ISCAS 96 (Cat. No.96CH35876). IEEE. Part vol.3, pp.178-181.

·          Dellnitz, M., Field, M., Golubitsky, M., Hohmann, A., Jun, M. [1995] "Cycling chaos," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.42, no.10, pp.821-823.

·          Dellnitz, M., Junge, O. [1997] "Almost invariant sets in Chua's circuit," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.7, no.11, pp.2475-2485.

·          Doerner, R., Hubinger, B., Martienssen, W. [1994] "Advanced chaos forecasting," Physical Review E. Statistical Physics, Plasmas, Fluids, & Related Interdisciplinary Topics, vol.50, no.1, pp.R12-15.

·          Duchesne, L. [1993] "Using Characteristic Multiplier Loci to Predict Bifurcation Phenomena and Chaos - a Tutorial," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.40, no.10, pp.683-688.

·          Eguchi, K., Inoue, T., Tsuneda, A. [1999] "Synthesis and analysis of a digital chaos circuit generating multiple-scroll strange attractors," IEICE Transactions on Fundamentals of Electronics Communications & Computer Sciences, vol.E82-A, no.6, pp.965-972.

·          Elgar, S., Chandran, V. [1993] "Higher Order Spectral Analysis of Chua's Circuit," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.40, no.10, pp.689-692.

·          Elgar, S., Vanhoff, B., Aguirre, L.A., Freitas, U.S., Chandran, V. [1998] "Higher-order spectra of nonlinear polynomial models for Chua's circuit," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.8, no.12, pp.2425-2431.

·          Elwakil, A.S., Kennedy, M.P. [1999] "Chaotic oscillator configuration using a frequency dependent negative resistor," Journal of Circuits Systems & Computers, vol.9, no.3-4, pp.229-242.

·          Femat, R., Alvarez-Ramirez, J., Castillo-Toledo, B., Gonzalez, J. [1999] "On robust chaos suppression in a class of nondriven oscillators: application to the Chua's circuit," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.46, no.9, pp.1150-1152.

·          Fortuna, L., Manganaro, G., Muscato, G., Nunnari, G. [1996] "Parallel simulation of cellular neural networks," Computers & Electrical Engineering, vol.22, no.1, pp.61-84.

·          Fradkov, A.L., Markov, A. [1997] "Adaptive synchronization of chaotic systems based on speed gradient method and passification," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.44, no.10, pp.905-912.

·          Galias, Z. [1997] "Positive topological entropy of Chua's circuit: a computer assisted proof," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.7, no.2, pp.331-349.

·          Galias, Z., Ogorzalek, M.J. [1999] "Study of synchronized motions in a one-dimensional array of coupled chaotic circuits," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.9, no.11, pp.2219-2224.

·          Ge, S.S., Wang, C. [1999] "Adaptive control of uncertain Chua's circuits," Proceedings of the 1999 IEEE International Symposium on Intelligent Control Intelligent Systems and Semiotics (Cat. No.99CH37014). IEEE. pp.126-131.

·          Genesio, R., Tesi, A., Villoresi, F. [1993] "A Frequency Approach for Analyzing and Controlling Chaos in Nonlinear Circuits," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.40, no.11, pp.819-828.

·          Gilli, M. [1995] "A spectral approach for studying spatio-temporal chaos," 1995 IEEE International Symposium on Circuits and Systems (Cat. No.95CH35771). IEEE. Part vol.1, pp.251-254.

·          Gilli, M. [1995] "Investigation of chaos in large arrays of Chua's circuits via a spectral technique," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.42, no.10, pp.802-806.

·          Gilli, M., Maggio, G.M. [1996] "Predicting chaos through an harmonic balance technique: an application to the time-delayed Chua's circuit," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.43, no.10, pp.872-874.

·          Gomez-Gesteira, M., Decastro, M., Perez-Villar, V. [1999] "On the role of random transversal uncoupling on re-entry formation," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.9, no.11, pp.2231-2236.

·          Gomez-Gesteira, M., Perez-Munuzuri, V., Chua, L.O., Perez-Villar, V. [1995] "Coexistence of excitability, Hopf and Turing modes in a one-dimensional array of nonlinear circuits," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.42, no.10, pp.672-677.

·          Gomez-Gesteirfa, M., deCastro, M., Perez-Villar, V., Chua, L.O. [1999] "Experimental Chua's circuit arrays as an autowave simulator," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.46, no.4, pp.495-499.

·          Goras, L., Chua, L.O. [1995] "Turing patterns in CNNs. II. Equations and behaviors," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.42, no.10, pp.612-626.

·          Goras, L., Chua, L.O. [1996] "Turing patterns in CNN's based on a new cell," 1996 Fourth IEEE International Workshop on Cellular Neural Networks and their Applications Proceedings (CNNA-96) (Cat. No.96TH8180). IEEE. pp.103-108.

·          Goras, L., Chua, L.O., Leenaerts, D.M.W. [1995] "Turing patterns in CNNs. I. Once over lightly," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.42, no.10, pp.602-611.

·          Gotz, M., Feldmann, U., Schwarz, W. [1993] "Synthesis of Higher Dimensional Chua Circuits," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.40, no.11, pp.854-860.

·          Grassi, G., Mascolo, S. [1998] "Design of nonlinear observers for hyperchaos synchronization using a scalar signal," Proceedings of the 1998 IEEE International Symposium on Circuits and Systems (Cat. No.98CH36187). IEEE. Part vol.3, pp.283-286.

·          Grassi, G., Mascolo, S. [1998] "Synchronization of hyperchaotic cellular neural networks: a system theory approach," 1998 IEEE International Joint Conference on Neural Networks Proceedings. IEEE World Congress on Computational Intelligence (Cat. No.98CH36227). IEEE. Part vol.2, pp.1504-1509.

·          Grassi, G., Mascolo, S. [1999] "Synchronizing high dimensional chaotic systems via eigenvalue placement with application to cellular neural networks," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.9, no.4, pp.705-711.

·          Guanrong, C. [1993] "Controlling Chua's Global Unfolding Circuit Family," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.40, no.11, pp.829-832.

·          Harada, Y., Masuda, K., Ogawa, A. [1996] "Dynamical behavior of acoustically coupled chaos oscillators," Fractals-An Interdisciplinary Journal on the Complex Geometry of Nature, vol.4, no.3, pp.407-414.

·          Hartley, T.T., Lorenzo, C.F., Killory Qammer, H. [1995] "Chaos in a fractional order Chua's system," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.42, no.8, pp.485-490.

·          Hartley, T.T., Mossayebi, F. [1995] "On the control of an array of Chua's systems," 1995 IEEE International Symposium on Circuits and Systems (Cat. No.95CH35771). IEEE. Part vol.2, pp.1536-1539.

·          Hein, S. [1993] "Exploiting Chaos to Suppress Spurious Tones in General Double-loop Sigma Delta Modulators," IEEE Transactions on Circuits & Systems II-Analog & Digital Signal Processing, vol.40, no.10, pp.651-659.

·          Hobson, P.R., Lansbury, A.N. [1996] "A simple electronic circuit to demonstrate bifurcation and chaos," Physics Education, vol.31, no.1, pp.39-43.

·          Hosny, E.A., Sobhy, M.I. [1994] "Analysis of chaotic behavior in lumped-distributed circuits applied to the time-delayed Chua's circuit," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.41, no.12, pp.915-918.

·          Hu, G., Jinghua, X., Chua, L.O., Pivka, L. [1998] "Controlling spiral waves in a model of two-dimensional arrays of Chua's circuits," Physical Review Letters, vol.80, no.9, pp.1884-1887.

·          Hu, G., Pivka, L, Zheleznyak, A.L. [1995] "Synchronization of a one-dimensional array of Chua's circuits by feedback control and noise," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.42, no.10, pp.736-740.

·          Huang, A. [1991] "Period Doubling and Period Plus One Law-chaotic Phenomena in Similar Chua's Circuit," China 1991 International Conference on Circuits and Systems. Conference Proceedings (Cat. No.91TH0387-1). IEEE. vol.2, pp.736-739.

·          Huang, A. [1996] "On bounds of the parametric range of bifurcation of Chua's circuit," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.43, no.8, pp.691-695.

·          Huang, An., Yang T. [1997] "Comment on "A new feedback control of a modified Chua's circuit system," Physica D, vol.102, no.3-4, pp.364-366.

·          Hwang, C.C., Chow, H.Y., Wang, Y.K. [1996] "A new feedback control of a modified Chua's circuit system," Physica D, vol.92, no.1-2, pp.95-100.

·          Hwang, C-C., Hsieh, J-Y., Lin, R-S. [1997] "A linear continuous feedback control of Chua's circuit," Chaos Solitons & Fractals, vol.8, no.9, pp.1507-1515.

·          Itoh, M. [1999] "Experimental study of impulsive synchronization," ISCAS'99. Proceedings of the 1999 IEEE International Symposium on Circuits and Systems VLSI (Cat. No.99CH36349). IEEE. Part vol.5, pp.410-413.

·          Itoh, M., Murakami, H. [1995] "New communication systems via chaotic synchronizations and modulations," IEICE Transactions on Fundamentals of Electronics Communications & Computer Sciences, vol.E78-A, no.3, pp.285-290.

·          Itoh, M., Murakami, H., Chua, L.O. [1994] "Communication systems via chaotic modulations," IEICE Transactions on Fundamentals of Electronics Communications & Computer Sciences, vol.E77-A, no.6, pp.1000-1006.

·          Itoh, M., Murakami, H., Chua, L.O. [1994] "Controlling chaotic motions in Chua's circuit via tunnels," 1994 IEEE International Symposium on Circuits and Systems (Cat. No.94CH3435-5). IEEE. Part vol.6, pp.89-92.

·          Itoh, M., Murakami, H., Chua, L.O. [1994] "Performance of Yamakawa's chaotic chips and Chua's circuits for secure communications," 1994 IEEE International Symposium on Circuits and Systems (Cat. No.94CH3435-5). IEEE. Part vol.6, pp.105-108.

·          Itoh, M., Murakami, H., Chua, L.O. [1994] "Secure communication systems via Yamakawa's chaotic chips and Chua's circuits," Proceedings of the Third IEEE Conference on Fuzzy Systems. IEEE World Congress on Computational Intelligence (Cat. No.94CH3430-6). IEEE. Part vol.2, pp.1293-1296.

·          Itoh, M., Murakami, H., Chua, L.O. [1995] "Signal transmission through a chain of Chua's circuits," 1995 IEEE International Symposium on Circuits and Systems (Cat. No.95CH35771). IEEE. Part vol.2, pp.1005-1008.

·          Itoh, M., Yang, T., Chua, L.O. [1999] "Experimental study of impulsive synchronization of chaotic and hyperchaotic circuits," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.9, no.7, pp.1393-1424.

·          Jia, X.D., Chen, R.M.M. [1994] "Design and simulation of nonlinear switched capacitor autonomous circuits containing nonlinear active resistor," 1994 IEEE International Symposium on Circuits and Systems (Cat. No.94CH3435-5). IEEE. Part vol.6, pp.165-168.

·          Jia, X.D., Chen, R.M.M. [1996] "Switched capacitor nonlinear circuits derived from Chua's circuit," 1996 IEEE International Symposium on Circuits and Systems. Circuits and Systems Connecting the World, ISCAS 96 (Cat. No.96CH35876). IEEE. Part vol.3, pp.213-216.

·          Jianxiong, X., Guanrong, C., Shieh, L.S. [1996] "Digital redesign for controlling the chaotic Chua's circuit," IEEE Transactions on Aerospace & Electronic Systems, vol.32, no.4, pp.1488-1500.

·          Johnston, G.A., Hunt, E.R. [1993] "Derivative Control of the Steady State in Chua's Circuit Driven in the Chaotic Region," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.40, no.11, pp.833-835.

·          Kaderka, J. [1996] "Modelling of third-order elementary canonical state models using cellular neural networks," Proceedings of the Third IEEE International Conference on Electronics, Circuits, and Systems. ICECS '96 (Cat. No.96TH8229). IEEE. Part vol.1, pp.295-298.

·          Kahan, S., Sicardi-Schifino, A.C. [1999] "Homoclinic bifurcations in Chua's circuit," Physica A, vol.262, no.1-2, pp.144-152.

·          Kapitaniak, T. [1995] "Experimental observation of riddled behaviour (electronic system)," Journal of Physics A-Mathematical & General, vol.28, no.3, pp.L63-66.

·          Kapitaniak, T., Chua, L.O., Zhong, G-Q. [1994] "Experimental hyperchaos in coupled Chua's circuits," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.41, no.7, pp.499-503.

·          Kapitaniak, T., Chua, L.O., Zhong, G-Q. [1997] "Experimental evidence of locally intermingled basins of attraction in coupled Chua's circuits," Chaos Solitons & Fractals, vol.8, no.9, pp.1517-1522.

·          Kavaslar, F., Guzelis, C. [1995] "A computer-assisted investigation of a 2-D array of Chua's circuits," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.42, no.10, pp.721-735.

·          Kawata, J., Nishio, Y., Ushida, A. [1996] "Analysis of Chua's circuit with transmission line," 1996 IEEE International Symposium on Circuits and Systems. Circuits and Systems Connecting the World, ISCAS 96 (Cat. No.96CH35876). IEEE. Part vol.3, pp.201-204.

·          Kawata, J., Nishio, Y., Ushida, A. [1997] "On the influence of transmission line on communication system using chaos synchronization," Proceedings of 1997 IEEE International Symposium on Circuits and Systems. Circuits and Systems in the Information Age. ISCAS '97 (Cat. No.97CH35987). IEEE. Part vol.2, pp.897-900.

·          Kawata,J., Nishio, Y., Ushida, A. [1997] "Analysis of Chua's circuit with transmission line," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.44, no.6, pp.556-558.

·          Kazantsev, V.B., Nekorkin, V.I., Velarde, M.G. [1997] "Pulses, fronts and chaotic wave trains in a one-dimensional Chua's lattice," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.7, no.8, pp.1775-1790.

·          Kennedy, M.P. [1993] "Three Steps to Chaos. I. Evolution," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.40, no.10, pp.640-656.

·          Kennedy, M.P. [1993] "Three Steps to Chaos. II. A Chua's Circuit Primer," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.40, no.10, pp.657-674.

·          Kennedy, M.P. [1994] "ABC (Adventures in Bifurcations and Chaos): a program for studying chaos," Journal of the Franklin Institute, vol.331B, no.6, pp.631-658.

·          Kennedy, M.P. [1995] "Experimental chaos from autonomous electronic circuits," Philosophical Transactions of the Royal Society of London a Mathematical & Physical Sciences, vol.353, no.1701, pp.13-32.

·          Kennedy, M.P. [1995] "On the relationship between the chaotic Colpitts oscillator and Chua's oscillator," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.42, no.6, pp.376-379.

·          Kevorkian, P. [1993] "Snapshots of Dynamical Evolution of Attractors from Chua's Oscillator," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.40, no.10, pp.762-780.

·          Konishi, K., Kawabata, H., Takeda, Y. [1994] "Control of Chua's circuit by switching a resistor," IEICE Transactions on Fundamentals of Electronics Communications & Computer Sciences, vol.E77-A, no.12, pp.2116-2119.

·          Kotaka, K., Inoue, T., Tsuneda, A. [1998] "A Design of CMOS Chua-type Analog Chaos Circuit Based on a Signal Flow Graph," IEICE Transactions on Fundamentals of Electronics Communications & Computer Sciences, vol.E81-A, no.7, pp.1533-1536.

·          Kozlov, A.K., Osipov, G.V., Shalfeev, V.D. [1997] "Suppressing chaos in continuous systems by impulse control," 1997 1st International Conference, Control of Oscillations and Chaos Proceedings (Cat. No.97TH8329). IEEE. Part vol.3, pp.578-581.

·          Krishchenko, A., Shalneva, S. [1999] "Localization problem for limit cycles of Chua circuit," ICECS'99. Proceedings of ICECS '99. 6th IEEE International Conference on Electronics, Circuits and Systems (Cat. No.99EX357). IEEE. Part vol.2, pp.647-650.

·          Kyprianidis, I.M., Petrani, M.L., Kalomiros, J.A., Anagnostopoulos, A.N. [1995] "Crisis-induced intermittency in a third-order electrical circuit," Physical Review E. Statistical Physics, Plasmas, Fluids, & Related Interdisciplinary Topics, vol.52, no.3, pt.A, pp.2268-2273.

·          Lakshmanan, M., Murali, K. [1995] "Experimental chaos from non-autonomous electronic circuits," Philosophical Transactions of the Royal Society of London a Mathematical & Physical Sciences, vol.353, no.1701, pp.33-46.

·          Lamarque, C-H., Janin, O., Awrejcewicz, J. [1999] "Chua systems with discontinuities," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.9, no.4, pp.591-616.

·          Lee, B-C., Lee, K-H., Wang, B-H. [1997] "Control bifurcation structure of return map control in Chua's circuit," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.7, no.4, pp.903-909.

·          Leenaerts, D.M.W. [1997] "Higher-order spectral analysis to detect power-frequency mechanisms in a driven Chua's circuit," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.7, no.6, pp.1431-1440.

·          Leuciuc, A. [1998] "The realization of inverse system for circuits containing nullors with applications in chaos synchronization," International Journal of Circuit Theory & Applications, vol.26, no.1, pp.1-12.

·          Liaw, Y-M., Tung, P-C. [1998] "Application of the differential geometric method to control a noisy chaotic system via dither smoothing," Physics Letters A, vol.239, no.1-2, pp.51-58.

·          Lin, G-N. [1991] "A Universal Circuit for Studying Chaos in Chua's Circuit Family," Proceedings of the 34th Midwest Symposium on Circuits and Systems (Cat. No.91CH3143-5). IEEE. vol.2., pp.772-775.

·          Lindberg, E. [1994] "Sinusoidal excitation on the Chua's circuit simulation of limit cycles and chaos," 1994 IEEE International Symposium on Circuits and Systems (Cat. No.94CH3435-5). IEEE. Part vol.6, pp.5-8.

·          Lindberg, E., Murali, K. [1998] "An eigenvalue study of the MLC circuit," 1998 IEEE International Conference on Electronics, Circuits and Systems. Surfing the Waves of Science and Technology (Cat. No.98EX196). IEEE. Part vol.2, pp.521-524.

·          Liu, J., Cai, T., Xiao, J., Zhang, Y., Wu, Y. [1996] "Chaos-shift-keying secure digital communications using feedback to synchronize Chua's circuit: simulation and realization," 1996 International Conference on Communication Technology Proceedings (Cat. No.96TH8118). IEEE. Part vol.1, pp.552-554.

·          Liu, J., Wu, Y.X., Xiao, J.H., Zhang, Y.H. [1996] "Multi-state chaos-shift-keying modulation system using feedback synchronising Chua's circuit," Electronics Letters, vol.32, no.8, pp.714-715.

·          Lorenzo, M.N., Marino, I.P., Perez-Munuzuri, V., Matias, M.A, Perez-Villar, V. [1996] "Synchronization waves in arrays of driven chaotic systems," Physical Review E. Statistical Physics, Plasmas, Fluids, & Related Interdisciplinary Topics, vol.54, no.4, pt.A, pp.R3094-3097.

·          Lozi, R. [1995] "Secure communications via chaotic synchronization in Chua's circuit and Bonhoeffer-Van der Pol equation: numerical analysis of the errors of the recovered signal," 1995 IEEE International Symposium on Circuits and Systems (Cat. No.95CH35771). IEEE. Part vol.1, pp.684-687.

·          Maayah, T.J., Khasawneh, M.A., Khadra, L.M. [1996] "A novel statistical approach for chaos detection in Chua's circuit," Proceedings of the Third IEEE International Conference on Electronics, Circuits, and Systems. ICECS '96 (Cat. No.96TH8229). IEEE. Part vol.2, pp.808-811.

·          Madan, R.N. [1992] "Observing and Learning Chaotic Phenomena from Chua's Circuit," Proceedings of the 35th Midwest Symposium on Circuits and Systems (Cat. No.92CH3099-9). IEEE. vol.1, pp.736-745.

·          Marino, I.P., Perez-Munuzuri, V., Matias, M.A. [1998] "Desynchronization transitions in rings of coupled chaotic oscillators," World Scientific. International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.8, no.8, pp.1733-1738.

·          Markov, A. [1997] "Adaptive synchronization of chaotic systems based on speed gradient method with application to communications," 1997 1st International Conference, Control of Oscillations and Chaos Proceedings (Cat. No.97TH8329). IEEE. Part vol.2, pp.376-378.

·          Marquez, R., Sira-Ramirez, H. [1995] "Nonlinear control of Chua's circuit," 38th Midwest Symposium on Circuits and Systems. Proceedings (Cat. No.95CH35853). IEEE. Part vol.1, pp.429-432.

·          Mascolo, S., Grassi, G. [1999] "Controlling chaotic dynamics using backstepping design with application to the Lorenz system and Chua's circuit," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.9, no.7, pp.1425-1434.

·          Matsumoto, T. [1984] "A Chaotic Attractor from Chua's Circuit," IEEE Transactions on Circuits & Systems, vol.CAS-31, no.12, pp.1055-1058.

·          Mayer-Kress, G., Choi, I., Weber, N., Barger, R., Hubler, A. [1993] "Musical Signals from Chua`s Circuit," IEEE Transactions on Circuits & Systems II-Analog & Digital Signal Processing, vol.40, no.10, pp.688-695.

·          McNames, J., Suykens, J.A.K., Vandewalle, J. [1999] "Winning entry of the K.U. Leuven time-series prediction competition," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.9, no.8, pp.1485-1500.

·          Meerkotter, K., Scholz, R. [1989] "Digital Simulation of Nonlinear Circuits by Wave Digital Filter Principles," Proceedings of 1989 IEEE International Symposium on Circuits and Systems (Cat. No.89CH2692-2). IEEE. vol.1, pp.720-723.

·          Mira, C. [1997] "Chua's circuit and the qualitative theory of dynamical systems," Elsevier. Journal of the Franklin Institute, vol.334B, no.5-6, pp.737-744.

·          Mira, C. [1997] "Chua's circuit and the qualitative theory of dynamical systems," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.7, no.9, pp.1911-1916.

·          Moreau, Y., Vandewalle, J. [1999] "Composition methods for the simulation of arrays of Chua's circuits," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.9, no.4, pp.723-733.

·          Morgul, O. [1995] "Inductorless realisation of Chua oscillator," Electronics Letters, vol.31, no.17, pp.1403-1404.

·          Morgul, O. [1995] "Wien bridge based RC chaos generator," Electronics Letters, vol.31, no.24, pp.2058-2059.

·          Morgul, O., Solak, E. [1996] "Observer based synchronization of chaotic systems," Physical Review E. Statistical Physics, Plasmas, Fluids, & Related Interdisciplinary Topics, vol.54, no.5, pp.4803-4811.

·          Morgul, O., Solak, E. [1997] "On the synchronization of chaotic systems by using state observers," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.7, no.6, pp.1307-1322.

·          Munuzuri, A.P., Chua, L.O. [1998] "Shortest-path-finder algorithm in a two-dimensional array of nonlinear electronic circuits," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.8, no.12, pp.2493-2501.

·          Munuzuri, A.P., deCastro, M., Perez-Munuzuri, V., Gomez-Gesteira, M., Marino, I.P., Hofer, E., Perez-Villar, V. [1996] "An electronic real-time model of one-dimensional discontinuous conduction of the cardiac impulse realized with Chua's circuits," 8th Mediterranean Electrotechnical Conference. Industrial Applications in Power Systems, Computer Science and Telecommunications. Proceedings (Cat. No.96CH35884). IEEE. Part vol.1, pp.439-442.

·          Munuzuri, A.P., Suykens, J.A.K., Chua, L.O. [1998] "A CNN approach to brain-like chaos-periodicity transitions," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.8, no.11, pp.2263-2278.

·          Murali, K., Lakshmanan, M. [1992] "Effect of Sinusoidal Excitation on the Chua's Circuit," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.39, no.4, pp.264-270.

·          Murali, K., Lakshmanan, M. [1993] "Chaotic Dynamics of the Driven Chua's Circuit," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.40, no.11, pp.836-840.

·          Murali, K., Lakshmanan, M. [1997] "Synchronization through compound chaotic signal in Chua's circuit and Murali-Lakshmanan-Chua circuit," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.7, no.2, pp.415-421.

·          Muruganandam, P., Murali, K., Lakshmanan, M. [1999] "Spatiotemporal dynamics of coupled array of Murali-Lakshmanan-Chua circuits," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.9, no.5, pp.805-830.

·          Neeley, J.E., Harris, J.G. [1996] "A subthreshold-CMOS chaotic oscillator," 1996 IEEE International Symposium on Circuits and Systems. Circuits and Systems Connecting the World, ISCAS 96 (Cat. No.96CH35876). IEEE. Part vol.3, pp.269-271.

·          Nekorkin, V.I., Kazantsev, V.B., Artyuhin, D.V. [1997] "Mutual synchronization of patterns and wave fronts in two coupled chains of Chua's circuits," 1997 1st International Conference, Control of Oscillations and Chaos Proceedings (Cat. No.97TH8329). IEEE. Part vol.1, pp.54-57.

·          Nekorkin, V.I., Kazantsev, V.B., Artyuhin, D.V., Velarde, M.G. [1999] "Wave propagation along interacting fiber-like lattices," European Physical Journal B, vol.11, no.4, pp.677-685.

·          Nekorkin, V.I., Kazantsev, V.B., Rulkov, N.F., Velarde, M.G., Chua, L.O. [1995] "Homoclinic orbits and solitary waves in a one-dimensional array of Chua's circuits," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.42, no.10, pp.785-801.

·          Nijimeijer, H. [1997] "On synchronization of chaotic systems," Proceedings of the 36th IEEE Conference on Decision and Control (Cat. No.97CH36124). IEEE. Part vol.1, pp.384-388.

·          Nossek, J.A. [1995] "Experimental verification of horseshoes from electronic circuits," Philosophical Transactions of the Royal Society of London a Mathematical & Physical Sciences, vol.353, no.1701, pp.59-64.

·          Ogorzalek, M.J. [1993] "Taming Chaos. I. Synchronization," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.40, no.10, pp.693-699.

·          Ogorzalek, M.J., Dabrowski, A., Dabrowski, W. [1994] "Hyperchaos, clustering and cooperative phenomena in CNN arrays composed of chaotic circuits," Proceedings of the Third IEEE International Workshop on Cellular Neural Networks and their Applications (CNNA-94) (Cat. No.94TH0693-2). IEEE. pp.315-20.

·          Ogorzalek, M.J., Galias, Z., Chua, L.O. [1993] "Exploring Chaos in Chua's Circuit Via Unstable Periodic Orbits," Proceedings of 1993 IEEE International Symposium on Circuits and Systems, vol.4, pp.2608-2611.

·          Ogorzalek, M.J., Galias, Z., Dabrowski, A.M., Dabrowski, W.R. [1995] "Chaotic waves and spatio-temporal patterns in large arrays of doubly-coupled Chua's circuits," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.42, no.10, pp.706-714.

·          Oksasoglu, A., Akgul, T. [1995] "Chaotic masking scheme with a linear inverse system," Physical Review Letters, vol.75, no.25, pp.4595-4597.

·          Oksasoglu, A., Huelsman, L.P. [1997] "Interaction of capacitive and resistive nonlinearities in Chua's circuit," Analog Integrated Circuits & Signal Processing, vol.12, no.3, pp.239-253.

·          Ono, Y., Fukushima, K. [1992] "A Scaling Property of the Fluctuation Spectrum for an Intermittency Observed in the Chua Circuit," Physics Letters A, vol.163, no.3, pp.173-175.

·          Osipov, G.V., Kozlov, A.K., Shalfeev, V.D. [1998] "Impulse control of chaos in continuous systems," Physics Letters A, vol.247, no.1-2, pp.119-128.

·          Osipov, G.V., Shalfeev, V.D. [1995] "Chaos and structures in a chain of mutually-coupled Chua's circuits," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.42, no.10, pp.693-699.

·          Osipov, G.V., Shalfeev, V.D. [1995] "The evolution of spatio-temporal disorder in a chain of unidirectionally-coupled Chua's circuits," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.42, no.10, pp.687-692.

·          Overfelt, P.L. [1999] "An electrically small dipole antenna loaded with Chua's oscillator: time-retarded chaos," IEEE Antennas and Propagation Society International Symposium. 1999 Digest. Held in conjunction with: USNC/URSI National Radio Science Meeting (Cat. No.99CH37010). IEEE. Part vol.4, pp.2872-2875.

·          Panas, A.I., Yang, T., Chua, L.O. [1998] "Experimental results of impulsive synchronization between two Chua's circuits," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.8, no.3, pp.639-644.

·          Parlitz, U., Junge, L., Kocarev, L. [1996] "Synchronization-based parameter estimation from time series," Physical Review E. Statistical Physics, Plasmas, Fluids, & Related Interdisciplinary Topics, vol.54, no.6, pp.6253-6259.

·          Perez-Marino, I., de Castro Rodriguez, M., Perez-Munuzuri, V., Gomez-Gesteira, M., Chua, L.O., Perez-Villar, V. [1995] "Study of reentry initiation in coupled parallel fibers (cardiology)," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.42, no.10, pp.665-671.

·          Perez-Munuzuri, A., Perez-Munuzuri, V., Perez-Villar, V., Chua, L.O. [1993] "Spiral Waves on a 2-D Array of Nonlinear Circuits," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.40, no.11, pp.872-877.

·          Perez-Munuzuri, V., Lorenzo, M.N. [1999] "Experimental improvement of chaotic synchronization due to multiplicative time-correlated Gaussian noise," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.9, no.12, pp.2321-2327.

·          Perez-Munuzuri, V., Munuzuri, A.P., Gomez-Gesteira, M., Perez-Villar, V., Pivka, L., Chua, L.O. [1995] "Nonlinear waves, patterns and spatio-temporal chaos in cellular neural networks," Philosophical Transactions of the Royal Society of London a Mathematical & Physical Sciences, vol.353, no.1701, pp.101-113.

·          Perez-Munuzuri, V., Perez-Villar, V., Chua, L.O. [1993] "Autowaves for image processing on a two-dimensional CNN array of excitable nonlinear circuits: flat and wrinkled labyrinths," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.40, no.3, pp.174-181.

·          Petrick, M.H., Wigdorowitz, B. [1997] "A priori nonlinear model structure selection for system identification," Control Engineering Practice, vol.5, no.8, pp.1053-1062.

·          Pinkney, J.Q., Camwell, P.L., Davies, R. [1995] "Chaos shift keying communications system using self-synchronising Chua oscillators," Electronics Letters, vol.31, no.13, pp.1021-1022.

·          Pivka, L, Wu, C-W., Huang, A. [1994] "Chua's oscillator: a compendium of chaotic phenomena," Journal of the Franklin Institute, vol.331B, no.6, pp.705-741.

·          Pivka, L. [1995] "Autowaves and spatio-temporal chaos in CNNs. I. A tutorial," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.42, no.10, pp.638-649.

·          Pivka, L. [1995] "Autowaves and spatio-temporal chaos in CNNs. II. A tutorial," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.42, no.10, pp.650-664.

·          Pospisil, J., Brzobohaty, J. [1996] "Elementary canonical state models of Chua's circuit family," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.43, no.8, pp.702-705.

·          Poznyak, A.S., Wen, Y., Sanchez, E.N. [1999] "Identification and control of unknown chaotic systems via dynamic neural networks," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.46, no.12, pp.1491-1495.

·          Rajasekar, S., Murali, K., Lakshmanan, M. [1997] "Control of chaos by nonfeedback methods in a simple electronic circuit system and the FitzHugh-Nagumo equation," Chaos Solitons & Fractals, vol.8, no.9, pp.1545-1558.

·          Ramesh, M., Narayanan, S. [1999] "Chaos control by nonfeedback methods in the presence of noise," Chaos Solitons & Fractals, Elsevier Science, vol.10, no.9, pp.1473-1489.

·          Rodet, X. [1993] "Models of musical instruments from Chua`s circuit with time delay," IEEE Transactions on Circuits & Systems II-Analog & Digital Signal Processing, vol.40, no.10, pp.696-701.

·          Rodriguez-Vazquez, A., Delgado-Restituto, M. [1993] "CMOS design of chaotic oscillators using state variables: a monolithic Chua`s circuit," IEEE Transactions on Circuits & Systems II-Analog & Digital Signal Processing, vol.40, no.10, pp.596-613.

·          Rodriguez-Vazquez, K., Fleming, P.J. [1999] "Genetic programming for dynamic chaotic systems modelling," Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406). IEEE. Part Vol.1, pp.22-28.

·          Romano, D., Bovati, M., Meloni, F. [1999] "Chua's atom," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.9, no.6, pp.1153-1157.

·          Rubchinsky, L., Sushchik, M. [1999] "Anomalous relationship between spatial and temporal patterns of dynamical behavior," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.9, no.12, pp.2329-2333.

·          Sanchez, E., Matias, M.A., Perez-Munuzuri, V. [1997] "Analysis synchronization of chaotic systems by noise: An experimental study," Physical Review E. Statistical Physics, Plasmas, Fluids, & Related Interdisciplinary Topics, vol.56, no.4, pp.4068-4071.

·          Sanchez, E., Matias, M.A., Perez-Munuzuri, V. [1999] "An experimental setup for studying the effect of noise on Chua's circuit," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.46, no.4, pp.517-520.

·          Sarafian, G., Kaplan, B.Z. [1995] "Is the Colpitts oscillator a relative of Chua's circuit?," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.42, no.6, pp.373-376.

·          Senani, R., Gupta, S.S. [1998] "Implementation of Chua's chaotic circuit using current feedback op-amps," Electronics Letters, vol.34, no.9, pp.829-830.

·          Sharkovsky, A.N. [1993] "Chaos from a time-delayed Chua's circuit," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.40, no.10, pp.781-783.

·          Sharkovsky, A.N., Chua, L.O. [1993] "Chaos in some 1-D discontinuous maps that appear in the analysis of electrical circuits," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.40, no.10, pp.722-731.

·          Shil'nikov, L.P. [1993] "Chua's circuit: rigorous results and future problems," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.40, no.10, pp.784-786.

·          Shuai, D., Watanabe, Y. [1994] "New hyper-distributed hyper-parallel AI approach based on chaotic bifurcations and synchronizations," 1994 IEEE International Conference on MFI '94. Multisensor Fusion and Integration for Intelligent Systems (Cat. No.94TH06965). IEEE. pp.410-416.

·          Spany, V., Pivka, L. [1993] "Two-segment bistability and basin structure in three-segment PWL circuits," IEE Proceedings-G Circuits Devices & Systems, vol.140, no.1, pp.61-67.

·          Suarez, A., Collantes, J-M. [1998] "Chaos detection in microwave circuits using harmonic balance commercial simulations," 1998 IEEE MTT-S International Microwave Symposium Digest (Cat. No.98CH36192). IEEE. Part vol.1, pp.271-274.

·          Suarez, A., Collantes, J-M. [1999] "A new technique for chaos prediction in RF circuit design using harmonic-balance commercial simulators," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.46, no.11, pp.1413-1415.

·          Suykens, J.A.K., Chua, L.O. [1997] "N-double scroll hypercubes in 1-D CNNs," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.7, no.8, pp.1873-1885.

·          Suykens, J.A.K., Curran, P.F., Chua, L.O. [1997] "Master-slave synchronization using dynamic output feedback," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.7, no.3, pp.671-679.

·          Suykens, J.A.K., Curran, P.F., Chua, L.O. [1999] "Robust synthesis for master-slave synchronization of Lur'e systems," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.46, no.7, pp.841-850.

·          Suykens, J.A.K., Curran, P.F., Vandewalle, J., Chua, L.O. [1997] "Robust nonlinear H_∞ synchronization of chaotic Lur'e systems," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.44, no.10, pp.891-904.

·          Suykens, J.A.K., Curran, P.F., Yang, T., Vandewalle, J., Chua, L.O. [1997] "Nonlinear H_∞ synchronization of Lur'e systems: dynamic output feedback case," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.44, no.11, pp.1089-1092.

·          Suykens, J.A.K., Vandewalle, J. [1993] "Generation of n-double scrolls (n=1, 2, 3, 4,...)," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.40, no.11, pp.861-867.

·          Suykens, J.A.K., Vandewalle, J. [1995] "Learning a simple recurrent neural state space model to behave like Chua's double scroll," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.42, no.8, pp.499-502.

·          Suykens, J.A.K., Vandewalle, J. [1997] "Master-slave synchronization of Lur'e systems," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.7, no.3, pp.665-669.

·          Suykens, J.A.K., Vandewalle, J., Chua, L.O. [1998] "Nonlinear H_∞ synchronization: case study for a hyperchaotic system," Proceedings of the 1998 IEEE International Symposium on Circuits and Systems (Cat. No.98CH36187). IEEE. Part vol.4, pp.572-575.

·          Suykens, J.A.K., Yang, T., Chua, L.O. [1998] "Impulsive synchronization of chaotic Lur'e systems by measurement feedback," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.8, no.6, pp.1371-1381.

·          Suykens, J.A.K., Yang, T., Vandewalle, J., Chua, L.O. [1998] "Impulsive synchronization of chaotic Lur'e systems: state feedback case," Proceedings of the 37th IEEE Conference on Decision and Control (Cat. No.98CH36171). IEEE. Part vol.2, pp.1963-1966.

·          Tang, K.S., Man, K.F. [1998] "An alternative Chua's circuit implementation," IEEE International Symposium on Industrial Electronics. Proceedings. ISIE'98 (Cat. No.98TH8357). IEEE. Part vol.2, pp.441-444.

·          Torres, L.A.B., Aguirre, L.A. [1999] "Extended chaos control method applied to Chua circuit," Electronics Letters, vol.35, no.10, pp.768-770.

·          Varone, A., Santoboni, G., Meloni, F. [1997] "The role of initial conditions in the synchronization problem," 1997 1st International Conference, Control of Oscillations and Chaos Proceedings (Cat. No.97TH8329). IEEE. Part vol.1, pp.42-45.

·          Volovodov, S., Lampe, B., Rozenvasser, Y. [1997] "Application of method of integral equations for analysis of complex periodic behaviors in Chua's circuits," 1997 1st International Conference, Control of Oscillations and Chaos Proceedings (Cat. No.97TH8329). IEEE. Part vol.1, pp.125-128.

·          Wang, H.O., Tanaka, K. [1996] "An LMI-based stable fuzzy control of nonlinear systems and its application to control of chaos," Proceedings of the Fifth IEEE International Conference on Fuzzy Systems. FUZZ-IEEE '96 (Cat. No.96CH35998). IEEE. Part vol.2, pp.1433-1438.

·          Wang, H.O., Tanaka, K., Ikeda, T. [1996] "Fuzzy modeling and control of chaotic systems," 1996 IEEE International Symposium on Circuits and Systems. Circuits and Systems Connecting the World, ISCAS 96 (Cat. No.96CH35876). IEEE. Part vol.3, pp.209-212.

·          Wang, X.F., Wang, Z.Q. [1998] "Synchronization of Chua's oscillators with the third state as the driving signal," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.8, no.7, pp.1599-1603.

·          Weigel, R., Jackson, E.A. [1998] "Experimental implementation of migrations in multiple-attractor systems," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.8, no.1, pp.173-178.

·          Wigdorowitz, B., Petrick, M.H. [1991] "Modelling Concepts Arising from an Investigation into a Chaotic System," Mathematical & Computer Modelling, vol.15, no.8, pp.1-16.

·          Wu, C.W., Rul'kov, N.F. [1993] "Studying chaos via 1-D maps-a tutorial," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.40, no.10, pp.707-721.

·          Wu, C-W., Chua, L.O. [1996] "On a conjecture regarding the synchronization in an array of linearly coupled dynamical systems," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.43, no.2, pp.161-165.

·          Yang, T., Chua, L.O. [1996] "Secure communication via chaotic parameter modulation," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.43, no.9, pp.817-819.

·          Yang, T., Chua, L.O. [1997] "Impulsive control and synchronization of nonlinear dynamical systems and application to secure communication," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.7, no.3, pp.645-664.

·          Yang, T., Chua, L.O. [1998] "Control of chaos using sampled-data feedback control," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.8, no.12, pp.2433-2438.

·          Yang, T., Chua, L.O. [1999] "Generalized synchronization of chaos via linear transformations," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.9, no.1, pp.215-219.

·          Yang, T., Y., Chua, L.O. [1997] "Impulsive stabilization for control and synchronization of chaotic systems: theory and application to secure communication," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.44, no.10, pp.976-988.

·          Yang, T., Yang, C-M., Yang, L-B. [1998] "A detailed study of adaptive control of chaotic systems with unknown parameters," Dynamics & Control, vol.8, no.3, pp.255-267.

·          Yin, Y-Z. [1997] "Experimental demonstration of chaotic synchronization in the modified Chua's oscillators," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.7, no.6, pp.1401-1410.

·          Yu, Z., Zhao, J. [1992] "Dynamic Behaviors in Two Novel Autonomous Circuits with a Physical Negative Resistor Characterized by Nonsymmetric Function," 1992 IEEE International Symposium on Circuits and Systems (Cat. No.92CH3139-3). IEEE. vol.6, pp.2813-2816.

·          Zhong, G.Q., Ko, K.T., Man, K.F. [1998] "Robustness of synchronization in coupled Chua's circuits," IEEE International Symposium on Industrial Electronics. Proceedings. ISIE'98 (Cat. No.98TH8357). IEEE. Part vol.2, pp.436-440.

·          Zhong, G-Q. [1994] "Implementation of Chua's circuit with a cubic nonlinearity," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.41, no.12, pp.934-941.

·          Zhong, G-Q., Ayrom, F. [1985] "Periodicity and chaos in Chua's circuit," IEEE Transactions on Circuits & Systems, vol.CAS-32, no.5, pp.501-503.

·          Zhong, G-Q., Bargar, R., Halle, K.S. [1994] "Circuits for voltage tuning the parameters of Chua's circuit: experimental application for musical signal generation," Journal of the Franklin Institute, vol.331B, no.6, pp.743-784.

·          Zhong, G-Q., Wu, C-W., Chua, L.O. [1998] "Torus-doubling bifurcations in four mutually coupled Chua's circuits," IEEE Transactions on Circuits & Systems I-Fundamental Theory & Applications, vol.45, no.2, pp.186-193.

·          Zhu, Z., Liu, Z. [1997] "Strange nonchaotic attractors of Chua's circuit with quasiperiodic excitation," International Journal of Bifurcation & Chaos in Applied Sciences & Engineering, vol.7, no.1, pp.227-238.

·          Zou, F., Nossek, J.A. [1992] "Double Scroll and Cellular Neural Networks," 1992 IEEE International Symposium on Circuits and Systems (Cat. No.92CH3139-3). IEEE. vol.1, pp.320-323.

Simplest Chaotic System with a Hyperbolic Sine

Simplest Chaotic System with a Hyperbolic Sine

Oscillating circuit using a TL084 op amp.
It's similar to Chua's Circuit with chaos, bifurcation, etc.

The two LEDs are there for use without an oscilloscope...here is a version by Sprott without LEDs: http://sprott.physics.wisc.edu/pubs/paper352.htm

I hate breadboards, oscillating circuits never seem to work, so here is my point-to-point wired beauty:

Ground clips from oscilloscope probes went to gathered ground wires from the op amp (which actually came off the positive output pins!). Clipped the probes onto the legs of a couple of the ceramic capacitors to take a reading.


Connected the two 9 volt batteries together and then ran positive wire and negative wire from the appropriate free battery posts.

Simple layout:

Good old TL084 pinout. I think I actually used TL084ACN (newer version):

Resistor R1 = 13kΩ,

All other resistors are 10kΩ.

All the capacitors are 0.01µF monolithic ceramic capacitors.

At first I kept getting the 'flying hotdog' which in the report of Liu, Sprott, Wang and Ma they accepted as a valid output. I was only getting it when nothing else was responding. Here is a pic of it, but it's not cool or interesting:






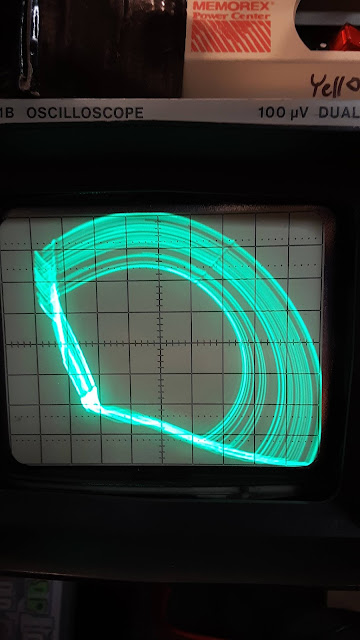
This is where the awesomeness starts! I had to touch my finger to the negative 9v battery output to get this circuit ring (actually it's a jerk circuit, so maybe it jerks?). This is because I didn't put a potentiometer at the double 9volt battery supply. It was full +/- 9 volts.



It is close to a chaotic attractor associated with a type I class 3 eigenvalue patttern.

This mimics (well, gets close anyway to) another valid response according to Liu et al's paper. It rarely showed up, because I wasn't varying the power supply much:

Chaos is a steady-state behavior possible in any nonlinear continuous system, if its order is above 2 in a forced circuit; or 3 in certain autonomous circuits.

 

We're just waiting for the thunder storm to pass by. 

BASIC vs SMALL BASIC 2020 Edition!!!

BASIC vs SMALL BASIC 2020 Edition!!!

So, here is an iterated logistic difference equation that I've posted about before showing animal population growth. I'm re-posting the old-timey BASIC version...and at the bottom giving the year 2019/2020 SMALL BASIC version that you can pop into Microsoft's still up and running (!) Small BASIC online app (there is a downloadable version too!).

First the original old-timey BASIC from 1980s version:

If you run it on an online BASIC simulator it works. For this, an online simulator works fine. Try this one:  https://repl.it/repls/InsignificantTepidEquipment


If you type "2" as your input the population hovers at around half an animal. If you type "5" as your starting population it goes to infinity (which is an error). So you need numbers less than 4 to keep it running true. The population levels out if you put in 1.5 as a start:


10 N=.1
20 INPUT"VALUE OF R";R
30 FOR I=1 TO 30
40 N1=R*N*(1-N)
50 PRINT N1
60 N=N1
70 NEXT I




Here is the screen capture of it in action:

Infinity: that's a lot of kitties! But an error in the program of going too high (R=5).

So here is R = 3.999

SMALL BASIC YEAR 2020 VERSION:

There is a new version of BASIC from Microsoft available as a download or an online simulator here: https://smallbasic-publicwebsite.azurewebsites.net/

It's called Small Basic...and the language is different!!! I had to use my mind-brain for about 2 minutes to port the program over (copy/paste, delete line numbers, search and find new variable command words like "textwindow.readnumber", etc.)


Here's a cut and paste version of the above script in the new language (it works, but doesn't give as many lines of results):

N=0.1

TextWindow.Write("What is the value of R? ")

R = TextWindow.ReadNumber()

FOR I=1 TO 30

N1=R*N*(1-N)

TextWindow.WriteLine("The result it " + N1 + ".")

N=N1

ENDfor

Each one of these lines is a seperate line in Small Basic (just number them 1, 2, 3, etc.) like this screenshot:

Oddly, it cannot handle decimals for the R value, so here is R=5:

Fun in (Small) BASIC for the year 2020!!!!!!!!!!!

How did I actually convert it? I pasted my old BASIC program into the new Microsoft Small Basic online window. It gave errors on almost every line.

Then I posted at the end a working program.

Then I compared them visually to see how they do know what they used to do and what new words (commands) did those things.  Old-timey "Print" became that "Textwindow.WriteLine" thing. Also, at the last line you must write "ENDfor" or else it won't run. Annoying but neat.

One day maybe I'll do the Fractal Mandelbrot program in the new Small Basic language.


Here's a cool modification that won't crash your computer since Small BASIC is modern:

N=0.1

TextWindow.Write("What is the value of R? ")

R = TextWindow.ReadNumber()

FOR I=1.00 TO 100.00

N1=R*N*(1-N)

TextWindow.WriteLine("The result it " + N1 + ".")

N=N1

ENDfor

See above, make the 4th line say "FOR I=1.00 to 100.00" and it will run a longer amount of lines.

You can make the second number 5000 and watch your computer just spew out the maths.

After a couple runs you need to copy and paste your program in again, it will stop working.

Of course, I wasn't saving and loading (or compiling) the program, just make changes. Copy,

click to reload the online simulator, re-paste in your program and make any changes. Annoying!

But fun.

-Happy Thanksgiving 2019!!!!